Categorías n-hereditarias.
| Dia | 2019-11-01 11:15:00-03:00 |
| Hora | 2019-11-01 11:15:00-03:00 |
| Lugar | Salón de seminarios del IMERL, Facultad de Ingeniería |
Categorías n-hereditarias.
Marco Pérez (IMERL)
El concepto de pureza juega un papel importante dentro del álgebra homológica en categorías de Grothendieck. De hecho, existen objetos en dichas categorías con buenas propiedades a la hora de estudiar sucesiones exactas puras. Sin embargo, normalmente uno se encuentra con ciertos agujeros en la literatura a la hora de buscar ejemplos de este tipo de sucesiones, y cuando las hay no siempre se tiene control sobre ellas.
Un escenario donde sí podemos tener control es cuando los objetos FP-inyectivos forman una clase de torsión. En este caso, para cada objeto  existe una sucesión exacta pura
existe una sucesión exacta pura %09%5Cto%09M%09%5Cto%09(1:%5Cmathbf%7Bt%7D)(M)%09%5Cto%090) , donde
, donde ) es FP-inyectivo.
es FP-inyectivo.
Recordamos de charlas anteriores que una generalización del escenario anterior se da por medio de los objetos 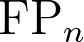 -inyectivos, ya que ellos forman una clase de torsión si, y solo si, los objetos de tipo
-inyectivos, ya que ellos forman una clase de torsión si, y solo si, los objetos de tipo 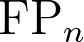 tienen dimensión proyectiva
tienen dimensión proyectiva  . Un ambiente para que esto ocurra es el de las categorías
. Un ambiente para que esto ocurra es el de las categorías  -hereditarias.
-hereditarias.
El objetivo de esta charla es dar aplicaciones y ejemplos de tal tipo de categorías. Nos enfocaremos en tres ejemplos conocidos de categorías de Grothendieck, y estudiaremos condiciones bajo las cuales ellas son  -hereditarias. A saber:
-hereditarias. A saber:
1. la categoría ) de complejos de cadena de
de complejos de cadena de  -módulos;
-módulos;
2. la categoría de funtores aditivos contravariantes ![[\Lambda^{\rm op},\mathsf{Ab}] [\Lambda^{\rm op},\mathsf{Ab}]](https://ci5.googleusercontent.com/proxy/Rutwbu24ZIIODBDWirysVs6BGdn1RJEeuOKHvrOLOPkfV4ejMk8emNI3xhvsR4ankOrH9aAbGE8Oz7D3pvGGiYJEO1Whl8wTy63Noa5PKIADZOD9Ym9NeqZ2isToX_PjiK7JdKDROvSWEgVzhqaxuSLh2b2PzjWAIMN73B6soiR08znWaU_ngs8=s0-d-e1-ft#https://s0.wp.com/latex.php?zoom=3&bg=transparent&fg=000000&s=0&latex=[%5CLambda%5E%7B%5Crm%09op%7D,%5Cmathsf%7BAb%7D]) , donde
, donde 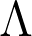 es una categoría aditiva esqueléticamente pequeña y
es una categoría aditiva esqueléticamente pequeña y 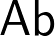 es la categoría de grupos abelianos; y
es la categoría de grupos abelianos; y
3. la categoría ) de haces casi-coherentes sobre un esquema casi-compacto y semi-separado
de haces casi-coherentes sobre un esquema casi-compacto y semi-separado  .
.
Veremos que ) nunca puede ser una categoría
nunca puede ser una categoría  -hereditaria. En cambio, probaremos que
-hereditaria. En cambio, probaremos que ![[\Lambda^{\rm op},\mathsf{Ab}] [\Lambda^{\rm op},\mathsf{Ab}]](https://ci5.googleusercontent.com/proxy/Rutwbu24ZIIODBDWirysVs6BGdn1RJEeuOKHvrOLOPkfV4ejMk8emNI3xhvsR4ankOrH9aAbGE8Oz7D3pvGGiYJEO1Whl8wTy63Noa5PKIADZOD9Ym9NeqZ2isToX_PjiK7JdKDROvSWEgVzhqaxuSLh2b2PzjWAIMN73B6soiR08znWaU_ngs8=s0-d-e1-ft#https://s0.wp.com/latex.php?zoom=3&bg=transparent&fg=000000&s=0&latex=[%5CLambda%5E%7B%5Crm%09op%7D,%5Cmathsf%7BAb%7D]) es
es  -hereditaria si, y solo si,
-hereditaria si, y solo si, 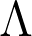 tiene pseudo núcleos con cierta condición de levantamiento. Finalmente, mostraremos que una condición suficiente para que
tiene pseudo núcleos con cierta condición de levantamiento. Finalmente, mostraremos que una condición suficiente para que ) sea
sea  -hereditaria es tener un cubrimiento finito afín y semi-separado de
-hereditaria es tener un cubrimiento finito afín y semi-separado de  tal que cada abierto del cubrimiento es homeomorfo al espectro de un anillo
tal que cada abierto del cubrimiento es homeomorfo al espectro de un anillo  -hereditario.
-hereditario.
[Trabajo conjunto con Daniel Bravo, Carlos E. Parra y Sinem Odabasi].
